Описательная статистика является важнейшей частью анализа данных, позволяя быстро выявить ключевые характеристики выборки. В Excel доступны мощные инструменты для вычисления таких статистических показателей, как среднее, медиана, стандартное отклонение и другие. Эти данные помогают понять структуру и распределение информации в вашем наборе данных, а также делают возможным выявление аномалий и трендов.
Для создания описательной статистики в Excel следует использовать встроенные функции и инструменты, такие как Среднее (AVERAGE), Медиану (MEDIAN), Стандартное отклонение (STDEV) и Минимум и максимум (MIN, MAX). Применение этих функций позволит вам получить важные количественные характеристики данных за считанные секунды. Например, для нахождения среднего значения в столбце с числовыми данными достаточно применить функцию =AVERAGE(диапазон), что быстро даст вам общее представление о величине, с которой работает ваш набор данных.
Для более комплексного анализа в Excel есть инструмент Анализ данных, который позволяет сгенерировать подробный отчет с множеством статистических показателей. Важно помнить, что использование этого инструмента требует предварительной настройки и включения соответствующей надстройки. Применение анализа данных даст вам не только простые средние значения, но и показатели, такие как асимметрия распределения, куртозис, а также корреляционные матрицы и другие важные параметры.
Как собрать данные для описательной статистики в Excel
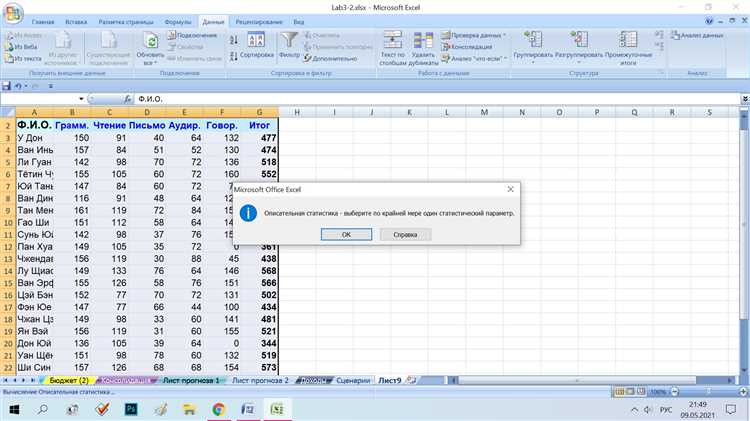
Для создания описательной статистики в Excel необходимо правильно собрать и подготовить данные, с которыми вы будете работать. Следует помнить, что данные должны быть точными и полными, чтобы результаты анализа были корректными. Основные этапы сбора данных включают:
1. Определение целей анализа. Прежде чем собирать данные, необходимо точно понять, какие вопросы вы хотите решить с помощью статистики. Это поможет выбрать подходящие данные и методы их сбора.
2. Источник данных. Выберите надежные источники для сбора информации. Это могут быть внутренние данные компании (например, продажи, отзывы клиентов, финансовые показатели) или внешние данные (например, исследования рынка, открытые статистические данные). Важно, чтобы данные были актуальными и достоверными.
3. Формат данных. Для работы в Excel данные должны быть представлены в удобном для анализа формате. Рекомендуется использовать таблицы с четко обозначенными столбцами и строками. Каждая строка должна представлять отдельный случай (например, один товар, один клиент, одно измерение), а каждый столбец – переменную, которую вы хотите анализировать (например, цена, возраст, количество).
4. Типы данных. Прежде чем собирать данные, определитесь с типом каждой переменной. В Excel данные могут быть числовыми (например, возраст, доход) или категориальными (например, пол, страна). Это важно для выбора методов статистического анализа и построения соответствующих графиков и диаграмм.
6. Организация данных в Excel. Как только данные собраны, поместите их в Excel в виде таблицы. Убедитесь, что каждый столбец имеет понятное название, а данные отсортированы по соответствующим признакам. Использование фильтров и сортировки облегчит работу с большими объемами информации и позволит выявить закономерности.
7. Преобразование данных. Если данные содержат категориальные переменные, их можно преобразовать в числовой формат для дальнейшего анализа. В Excel это можно сделать с помощью функции поиска (например, VLOOKUP) или формул для создания сводных данных.
8. Обработка пропусков. Важно заранее определиться с тем, как вы будете обрабатывать пропуски в данных. В Excel существует несколько способов: заменять пропущенные значения средними, медианными значениями или просто удалять такие строки или столбцы, если это не приведет к потере важной информации.
После того как данные собраны и организованы, можно приступать к их анализу и созданию описательной статистики в Excel. Для этого можно использовать встроенные функции и инструменты Excel, такие как среднее значение, медиана, стандартное отклонение, а также построение гистограмм и диаграмм для визуализации данных.
Как использовать функцию СРЗНАЧ для расчета среднего значения
Функция СРЗНАЧ в Excel применяется для вычисления среднего значения числовых данных в заданном диапазоне. Чтобы использовать эту функцию, достаточно ввести формулу в ячейку, и программа автоматически подсчитает среднее арифметическое всех значений в указанном диапазоне.
Пример: если в ячейках A1:A5 находятся числа 5, 10, 15, 20 и 25, то формула =СРЗНАЧ(A1:A5) вернет результат 15, так как это среднее значение всех этих чисел. Важно, что функция игнорирует пустые ячейки и текстовые данные, поэтому они не влияют на расчет.
Чтобы убедиться, что функция работает корректно, стоит обратить внимание на следующие моменты:
- Диапазон данных должен содержать числовые значения. Если в диапазоне есть текст или логические значения, их можно исключить с помощью других функций.
- Если диапазон данных включает ошибки, например, #DIV/0! или #VALUE!, функция вернет ошибку. Для обработки ошибок можно использовать функцию ЕСЛИОШИБКА.
Для более сложных расчетов можно комбинировать функцию СРЗНАЧ с другими функциями, например, ЕСЛИ для вычисления среднего только по тем значениям, которые соответствуют заданному условию. Формула =СРЗНАЧ(ЕСЛИ(A1:A10>10, A1:A10)) позволит рассчитать среднее значение только для чисел, которые больше 10.
Функция СРЗНАЧ является одним из самых простых и быстрых инструментов для анализа данных, особенно если необходимо получить общее представление о тенденциях в числовых показателях.
Как вычислить медиану с помощью функции МЕДИАНА
Функция МЕДИАНА в Excel используется для вычисления медианы набора данных, то есть числа, которое делит отсортированный ряд данных пополам. Медиана может быть полезной для анализа данных, когда необходимо исключить влияние экстремальных значений, таких как выбросы.
Для использования функции МЕДИАНА в Excel необходимо выполнить следующие шаги:
- Выберите ячейку, в которой хотите отобразить медиану.
- Введите формулу
=МЕДИАНА(диапазон), гдедиапазон– это диапазон ячеек, содержащих данные, для которых вы хотите найти медиану. - Нажмите Enter.
Пример:
Если данные находятся в ячейках A1:A10, то для вычисления медианы нужно ввести формулу: =МЕДИАНА(A1:A10).
Если в наборе данных нечётное количество значений, медианой будет среднее значение, которое стоит посередине отсортированного списка. Если количество значений чётное, медиана рассчитывается как среднее значение двух центральных элементов.
- Пример с нечётным количеством значений: если набор данных 3, 5, 7, медиана – 5.
- Пример с чётным количеством значений: если набор данных 1, 3, 5, 7, медиана – (3 + 5) / 2 = 4.
Функция МЕДИАНА также учитывает пустые ячейки в диапазоне, игнорируя их при расчёте, и может работать с числами, текстовыми значениями или ошибками в ячейках.
Для более точного анализа медианы важно предварительно отсортировать данные. Однако Excel автоматически обработает данные и вычислит медиану независимо от порядка чисел в диапазоне.
Как найти стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН
Функция СТАНДОТКЛОН в Excel позволяет вычислить стандартное отклонение выборки, что полезно для анализа разброса данных. Для того чтобы получить результат, нужно выполнить несколько простых шагов:
- Подготовка данных: Убедитесь, что данные, по которым нужно рассчитать стандартное отклонение, находятся в одном столбце или строке. Например, пусть данные лежат в ячейках A1:A10.
- Использование функции: В нужной ячейке введите формулу
=СТАНДОТКЛОН(A1:A10), где A1:A10 – это диапазон ячеек с вашими данными. - Обработка результата: После нажатия Enter в ячейке отобразится значение стандартного отклонения для указанного диапазона.
Также стоит учитывать несколько нюансов при использовании этой функции:
- Диапазон данных: Функция работает только с числовыми значениями. Если в диапазоне есть текст или пустые ячейки, Excel игнорирует их при вычислениях.
- Тип выборки: Функция СТАНДОТКЛОН используется для вычисления стандартного отклонения выборки, а не генеральной совокупности. Если вам нужно вычислить стандартное отклонение для всей совокупности данных, используйте функцию СТАНДОТКЛОН.П.
- Точность: Чем больше количество данных, тем более точным будет расчет стандартного отклонения. Для небольших выборок результат может быть менее точным.
Для различных типов данных в Excel есть несколько вариантов функций для стандартного отклонения:
- СТАНДОТКЛОН.СТ (STDEV.S): Для выборки данных. Используется по умолчанию в версии Excel 2010 и более поздних версиях.
- СТАНДОТКЛОН.П (STDEV.P): Для всего массива данных (генеральной совокупности), если известны все значения.
Таким образом, функция СТАНДОТКЛОН – это простой, но мощный инструмент для анализа разброса данных в Excel. Следуйте этим рекомендациям для точных и эффективных расчетов.
Как рассчитать минимальное и максимальное значения с помощью функций МИН и МАКС
Функции МИН и МАКС в Excel используются для нахождения наименьшего и наибольшего значения в диапазоне данных. Эти функции полезны при анализе больших массивов информации и позволяют быстро получить ключевые статистические показатели.
Для использования функции МИН необходимо ввести в ячейку следующее выражение: =МИН(A1:A10), где A1:A10 – это диапазон ячеек, для которого требуется найти минимальное значение. Функция автоматически вернет наименьшее число из выбранного диапазона.
Аналогично, функция МАКС используется для нахождения максимального значения. Для этого достаточно ввести формулу: =МАКС(B1:B10), где B1:B10 – диапазон данных, из которого Excel определит наибольшее значение.
Важно помнить, что если в диапазоне присутствуют текстовые данные или пустые ячейки, они игнорируются при расчетах, и функция возвращает результат, опираясь только на числовые значения.
Если необходимо вычислить минимальное или максимальное значение с учетом нескольких диапазонов, можно указать их через запятую. Например, =МИН(A1:A10, B1:B10) вернет минимальное значение среди всех чисел, расположенных в двух указанных диапазонах.
Использование этих функций существенно ускоряет анализ данных, минимизируя возможные ошибки при ручном подсчете. Это особенно актуально при работе с большими объемами данных в финансовых отчетах, базах данных и статистических исследованиях.
Как построить диаграмму для визуализации описательной статистики

1. Выделите данные, которые необходимо визуализировать. Для построения диаграммы можно использовать числовые данные, такие как возраст, доходы или любые другие измерения.
2. На вкладке «Вставка» выберите тип диаграммы. Если ваша задача – показать распределение, выберите гистограмму. Если хотите продемонстрировать вариации или аномалии в наборе данных, используйте коробчатую диаграмму. Для сравнения статистических значений между категориями используйте столбчатую диаграмму.
3. После создания диаграммы на панели инструментов «Конструктор» настройте ее. Добавьте заголовки осей для более точного восприятия данных. Для того чтобы выделить ключевые моменты, можно использовать подписи данных.
4. Для анализа медианы и квартилей полезно добавить линию на коробчатую диаграмму, которая покажет важные значения в наборе данных. Используя параметры диаграммы, можно настроить цвет, тип линии и другие характеристики для лучшей читаемости.
5. При необходимости отрегулируйте диапазон значений на осях, чтобы сделать график более информативным. Например, если значения сильно различаются, настройка оси Y поможет более детально отобразить изменения.
6. Наконец, для улучшения восприятия диаграммы рекомендуется использовать цветовую кодировку или выделение ключевых статистических меток (например, среднее или стандартное отклонение), чтобы аудитория могла быстро ориентироваться в данных.
Как интерпретировать результаты описательной статистики в Excel
Среднее значение представляет собой центральную тенденцию набора данных, показывая среднюю величину всех наблюдений. Оно особенно полезно, когда данные распределены нормально, без сильных отклонений. Если среднее значительно отличается от медианы, это может свидетельствовать о наличии выбросов или асимметрии в данных.
Медиана – это значение, которое делит данные пополам. Она особенно полезна при наличии выбросов, так как медиана менее чувствительна к экстремальным значениям, чем среднее. Когда медиана существенно отличается от среднего, это может быть индикатором того, что распределение данных несимметрично.
Мода показывает наиболее часто встречающееся значение в выборке. Если мода совпадает с медианой и средним, распределение данных близко к нормальному. В случае, если существует несколько мод, это может свидетельствовать о многомодальном распределении данных, требующем дополнительного анализа.
Стандартное отклонение характеризует, насколько сильно данные отклоняются от среднего. Низкое стандартное отклонение указывает на малые колебания данных, а высокое – на большую изменчивость. Для интерпретации стандартного отклонения важно сравнивать его с средним значением. Большие отклонения могут быть результатом экстремальных значений или необычного распределения.
Дисперсия – это квадрат стандартного отклонения. Она используется для измерения разброса значений, но в отличие от стандартного отклонения, не имеет интуитивно понятной единицы измерения. Оценка дисперсии помогает понять степень вариативности в наборе данных, но стандартное отклонение более информативно для повседневных анализов.
Минимум и максимум определяют диапазон значений в данных. Анализ этих показателей в сочетании с другими статистическими параметрами позволяет выявить возможные выбросы. Если минимум или максимум сильно отклоняются от остальной части данных, это может быть сигналом для дальнейшего исследования.
Коэффициент вариации помогает сравнивать разброс данных между различными наборами, особенно если их средние значения значительно различаются. Он показывает, насколько велико стандартное отклонение относительно среднего значения и полезен для сопоставления данных с разными масштабами.
Вопрос-ответ:
Что такое описательная статистика в Excel и для чего она используется?
Описательная статистика в Excel позволяет на основе набора данных рассчитывать основные статистические показатели, такие как среднее значение, медиана, стандартное отклонение, минимум и максимум. Эти показатели помогают понять основные характеристики данных, выявить закономерности и сделать предварительные выводы о них. Например, если у вас есть список оценок студентов, с помощью описательной статистики можно быстро оценить, как в среднем справляются ученики и насколько эти оценки разнообразны.
Как в Excel рассчитать среднее значение набора данных?
Для того чтобы рассчитать среднее значение, нужно использовать функцию СРЕДНЕЕ (AVERAGE). Просто выделите диапазон ячеек, который содержит числовые значения, и введите формулу =СРЕДНЕЕ(A1:A10), где A1:A10 — это диапазон данных. Excel автоматически вычислит среднее значение для всех чисел в указанном диапазоне.
Какие еще функции Excel могут помочь в анализе данных для построения описательной статистики?
Помимо функции СРЕДНЕЕ, в Excel есть множество других полезных функций для описательной статистики. Например, для вычисления медианы можно использовать функцию МЕДИАНА. Для нахождения стандартного отклонения подойдет функция СТАНДОТКЛОН (STDEV). Если нужно найти наименьшее или наибольшее значение в наборе данных, используйте функции МИН и МАКС. Эти функции помогут не только понять, как распределены данные, но и выделить наиболее важные элементы набора данных.
Можно ли в Excel создать сводную таблицу для построения описательной статистики?
Да, сводные таблицы в Excel являются отличным инструментом для агрегирования данных и проведения описательной статистики. С их помощью можно легко группировать данные по категориям и вычислять различные статистические показатели, такие как сумма, среднее, минимумы и максимумы для каждой категории. Для этого выберите данные, затем в разделе «Вставка» выберите «Сводная таблица», и после этого перетащите нужные поля в области строк и значений.
Как визуализировать результаты описательной статистики в Excel?
Для визуализации результатов описательной статистики в Excel можно использовать диаграммы и графики. Например, для отображения распределения данных можно создать гистограмму с помощью вкладки «Вставка» и выбрать соответствующий тип графика. Диаграммы помогают наглядно увидеть, как распределены данные, выявить выбросы и тенденции, что делает анализ более понятным и доступным для восприятия.
Как можно создать описательную статистику в Excel для набора данных?
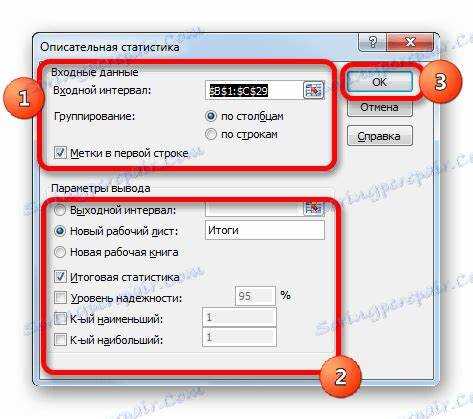
Для того чтобы создать описательную статистику в Excel, можно использовать функцию «Анализ данных», которая доступна через вкладку «Данные». Сначала необходимо выбрать диапазон ячеек с вашими данными, затем перейти в меню «Данные», выбрать «Анализ данных», а из предложенного списка выбрать пункт «Описательная статистика». В открывшемся окне можно выбрать нужные параметры, такие как среднее значение, стандартное отклонение, минимальные и максимальные значения и другие метрики. После этого нажмите «ОК», и Excel автоматически создаст сводку по вашему набору данных.
Как в Excel рассчитать стандартное отклонение для набора данных?
Для того чтобы рассчитать стандартное отклонение в Excel, можно воспользоваться встроенной функцией. Для этого выберите ячейку, в которой хотите увидеть результат, и введите формулу: =СТАНДОТКЛОН(диапазон_данных). Например, если ваши данные находятся в ячейках A1:A10, формула будет выглядеть так: =СТАНДОТКЛОН(A1:A10). После нажатия Enter Excel рассчитает стандартное отклонение для указанного диапазона данных. Стандартное отклонение показывает, насколько сильно данные отклоняются от среднего значения, что позволяет лучше понять вариативность данных.