Как реализовать граф на python

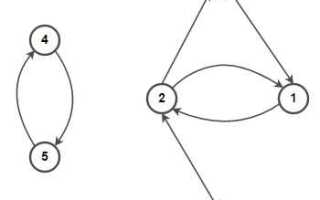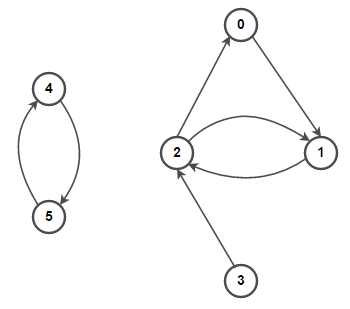
Графы являются важной частью теории графов и широко используются для представления различных объектов и их взаимосвязей. В Python существует несколько библиотек, которые позволяют легко создавать и работать с графами. В этой статье мы рассмотрим, как можно построить граф с использованием популярной библиотеки NetworkX.

Для создания графа в Python вам потребуется знание основ теории графов и базовых понятий, таких как вершины и рёбра. В Python граф можно представить с помощью различных структур данных, но NetworkX предоставляет удобный и мощный интерфейс для реализации графов разных типов. Он позволяет создавать как направленные, так и ненаправленные графы, работать с аттрибутами вершин и рёбер, а также анализировать свойства графов.

В этой статье мы покажем, как с помощью NetworkX создать простой граф, добавить вершины и рёбра, а также визуализировать результат. Вы научитесь строить графы для решения реальных задач и анализировать их с помощью Python. Для начала достаточно установить библиотеку с помощью pip и импортировать её в код.

Установка необходимых библиотек для построения графов

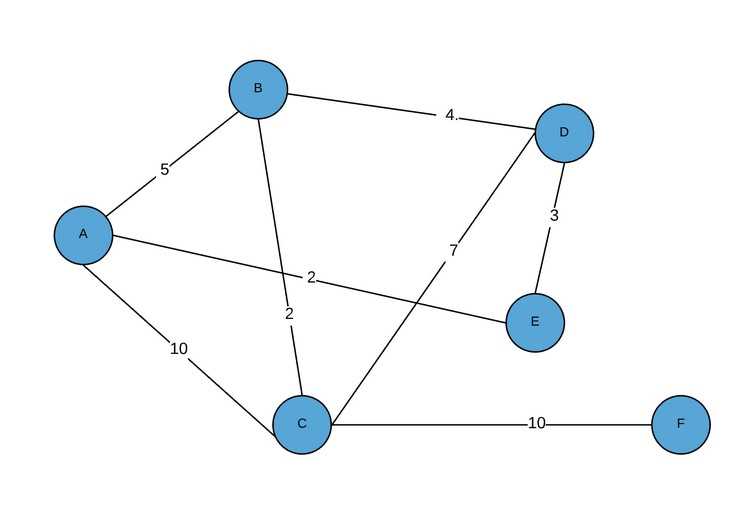
Для построения графов в Python необходимо установить несколько ключевых библиотек, которые обеспечат удобство работы с данными и визуализацией графов.

Одной из самых популярных библиотек является NetworkX, предназначенная для создания, манипулирования и анализа структуры графов. Для ее установки используйте команду:

pip install networkx

Еще одной важной библиотекой является Matplotlib, которая используется для визуализации графов. Установка выполняется следующей командой:

pip install matplotlib

В случае необходимости улучшенной визуализации можно использовать библиотеку Plotly, которая позволяет строить интерактивные графики. Установить её можно через:

pip install plotly

Для работы с графами, представленных в виде сетей, можно также установить библиотеку Graph-tool, которая предоставляет продвинутые методы для анализа графов. Она устанавливается с помощью:

pip install graph-tool

После установки этих библиотек можно приступать к построению и анализу графов в Python.

Создание графа с использованием библиотеки NetworkX

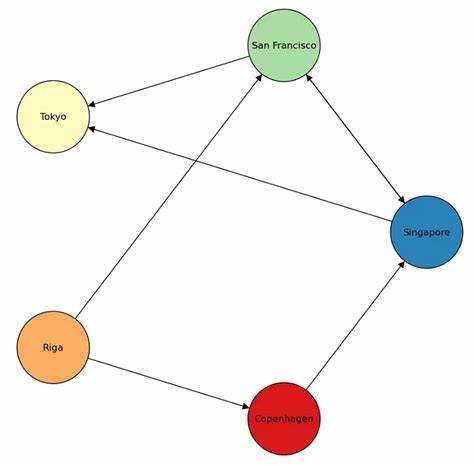
Библиотека NetworkX предоставляет удобные средства для работы с графами в Python. Она позволяет создавать, анализировать и визуализировать графы различных типов. С помощью этой библиотеки можно работать с ориентированными и неориентированными графами, а также выполнять различные алгоритмические операции.

Для начала работы с NetworkX необходимо установить саму библиотеку. Это можно сделать с помощью pip:

pip install networkx

После установки можно приступать к созданию графа. Рассмотрим пример создания простого графа.

Создание графа

Для создания графа необходимо создать объект класса граф. Например, для создания неориентированного графа:

import networkx as nx
G = nx.Graph()

Для создания ориентированного графа используется класс DiGraph:

G = nx.DiGraph()

Добавление узлов и рёбер

Узлы добавляются в граф с помощью метода add_node, а рёбра – с помощью метода add_edge.

• Добавление одного узла:

G.add_node(1)

• Добавление нескольких узлов:

G.add_nodes_from([2, 3, 4])

• Добавление одного ребра:

G.add_edge(1, 2)

• Добавление нескольких рёбер:

G.add_edges_from([(2, 3), (3, 4)])

Просмотр информации о графе

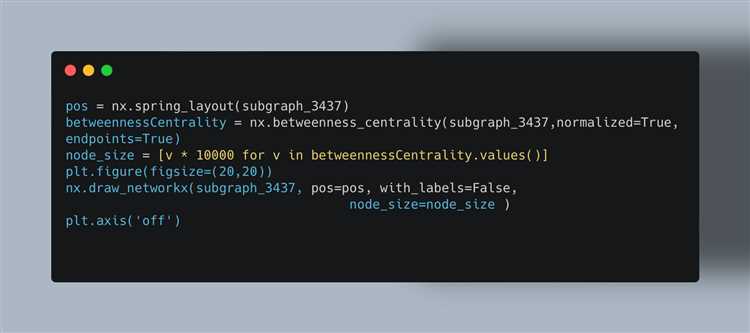
Для получения информации о графе можно использовать следующие методы:

• G.nodes – возвращает все узлы графа.
• G.edges – возвращает все рёбра графа.
• G.degree – возвращает степень узла (количество рёбер, инцидентных узлу).

Пример:

Визуализация графа

Для визуализации графа можно использовать библиотеку Matplotlib. Визуализация создается с помощью метода draw:

import matplotlib.pyplot as plt
nx.draw(G, with_labels=True)
plt.show()

Этот код отобразит граф с метками для каждого узла.

Работа с аттрибутами узлов и рёбер

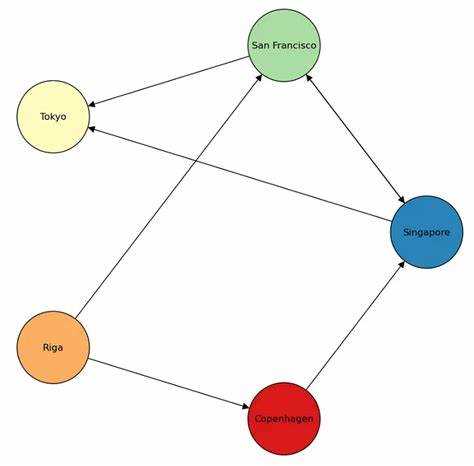
Можно добавлять атрибуты к узлам и рёбрам графа, чтобы хранить дополнительные данные.

• Добавление атрибута к узлу:

G.nodes[1]['color'] = 'red'

• Добавление атрибута к ребру:

G[1][2]['weight'] = 4.2

Для получения атрибутов используйте доступ через ключи:

Заключение

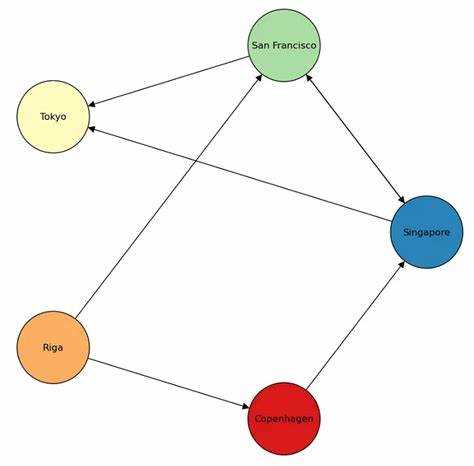
Библиотека NetworkX предоставляет широкие возможности для работы с графами, включая создание, добавление узлов и рёбер, визуализацию, а также работу с аттрибутами. Она является мощным инструментом для решения задач, связанных с графами в Python.

Визуализация графа с помощью Matplotlib

Для того чтобы визуализировать граф, необходимо использовать модуль `networkx`, который хорошо интегрируется с Matplotlib. Сначала создается граф с помощью `networkx`, а затем его визуализация с использованием функций Matplotlib.

Пример простого кода для визуализации графа:

import networkx as nx
import matplotlib.pyplot as plt
# Создаем граф
G = nx.erdos_renyi_graph(10, 0.5)
# Визуализируем граф
nx.draw(G, with_labels=True)
plt.show()

В данном примере создается случайный граф с 10 вершинами, и с помощью функции `nx.draw` выполняется его визуализация. Опция `with_labels=True` добавляет метки на вершины.

Matplotlib позволяет детально настраивать внешний вид графа. Можно изменять цвета узлов, рёбер, а также их форму и стиль. Для настройки можно использовать дополнительные параметры в методах библиотеки, например, задавать цвет рёбер, размер узлов и их метки.

Также можно применить различные алгоритмы расположения для более эффективной визуализации сложных графов, такие как `spring_layout`, `circular_layout`, `kamada_kawai_layout` и другие. Эти алгоритмы помогают располагать узлы в более информативных и понятных формах.

Таким образом, Matplotlib предоставляет мощные инструменты для визуализации графов, позволяя адаптировать отображение под нужды пользователя и делать анализ данных более наглядным.

Добавление узлов и рёбер в граф Python

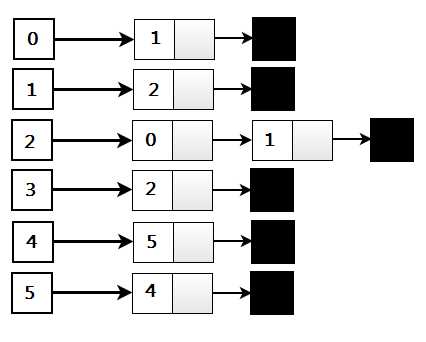
Для создания графа в Python часто используется библиотека NetworkX. В этой библиотеке можно легко добавить узлы и рёбра, что позволяет гибко работать с графами.

Чтобы добавить узлы, можно использовать метод add_node(). Он позволяет добавить один узел в граф. Например, для добавления узла с именем «A» нужно написать:

G.add_node("A")

Можно также добавить несколько узлов одновременно, передав их в виде списка:

G.add_nodes_from(["B", "C", "D"])

Для добавления рёбер используется метод add_edge(). Этот метод принимает два аргумента – узлы, которые будут связаны рёбером. Например, чтобы добавить рёбер между узлами «A» и «B», можно использовать следующий код:

G.add_edge("A", "B")

Если необходимо добавить сразу несколько рёбер, это можно сделать с помощью метода add_edges_from(), передав список рёбер:

G.add_edges_from([("A", "B"), ("B", "C"), ("C", "A")])

Методы add_node() и add_edge() позволяют создавать как ориентированные, так и неориентированные графы в зависимости от конфигурации графа.

Работа с направленными и ненаправленными графами

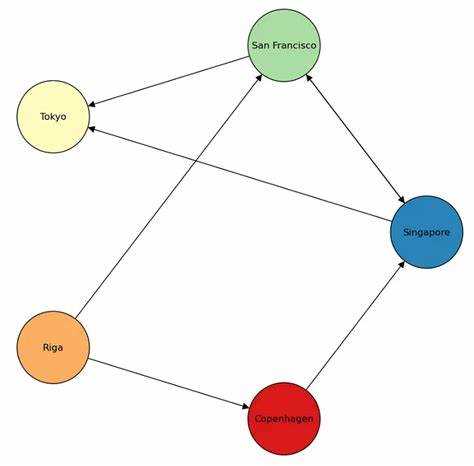
В Python для создания графов можно использовать различные библиотеки, такие как NetworkX, которая позволяет работать как с направленными, так и с ненаправленными графами. Направленные и ненаправленные графы имеют несколько отличий, которые важно учитывать при работе с ними.

Направленный граф (directed graph) – это граф, в котором рёбра имеют направление. Каждый рёбро в таком графе представляет собой пару вершин, и направление указывает на то, от какой вершины к какой происходит переход.

• Направление рёбер помогает моделировать системы, где отношения между объектами имеют направленность (например, в социальных сетях, где один пользователь может подписаться на другого).
• В таких графах важно учитывать направление перехода, а не только наличие связи.

Ненаправленный граф (undirected graph) – это граф, в котором рёбра не имеют направления. Соединение между двумя вершинами означает наличие отношения между ними, но не определяет, в каком направлении оно происходит.

• Ненаправленные графы обычно применяются для моделирования отношений, где важен только факт существования связи между объектами (например, в моделях отношений между людьми в графах дружбы).
• В таких графах рёбра двусторонние, то есть для каждой пары вершин существует только одно ребро, независимо от направления.

Основные методы работы с направленными и ненаправленными графами:

1. Создание графа: Для создания графа используется класс Graph (ненаправленный граф) или DiGraph (направленный граф) из библиотеки NetworkX.
2. Добавление рёбер: В ненаправленном графе рёбра добавляются через метод add_edge, а в направленном графе также используется этот метод, но добавляется указание направления.
3. Поиск путей: В направленных графах важно учитывать направление при поиске путей между вершинами, в то время как в ненаправленных графах направление не имеет значения.
4. Анализ связности: В ненаправленных графах анализируется общая связность, тогда как в направленных графах может быть важно анализировать компоненты сильной и слабой связности.

Пример создания направленного и ненаправленного графа в Python:

import networkx as nx
# Создание ненаправленного графа
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3), (3, 4)])
# Создание направленного графа
DG = nx.DiGraph()
DG.add_edges_from([(1, 2), (2, 3), (3, 4)])

При работе с графами важно правильно выбрать тип графа в зависимости от задачи. Направленные графы подходят для моделирования процессов с явным направлением, в то время как ненаправленные графы используются для отображения связей, где направление не имеет значения.

Анализ графа: поиск путей и вычисление центральности

Поиск путей в графе является основой для решения задач, таких как нахождение кратчайшего пути, определение маршрутов и оптимизация сетевых потоков. Основные алгоритмы поиска путей включают алгоритм Дейкстры, который находит кратчайший путь между вершинами с учетом весов рёбер, и алгоритм поиска в глубину (DFS), который полезен для нахождения всех путей от одной вершины к другой в ориентированных или неориентированных графах.

Алгоритм Дейкстры работает с графами, где рёбра имеют ненегативные веса, и его цель – найти кратчайшие пути от исходной вершины до всех остальных. Время работы алгоритма зависит от структуры графа и выбранной реализации, но в общем случае оно составляет O(E + V log V), где E – количество рёбер, а V – количество вершин.

Центральность графа измеряет «важность» или «влияние» вершин в структуре сети. Существует несколько методов для вычисления центральности, включая степень вершины, близость, посредничество и собственную центральность.

Центральность по степени определяется количеством рёбер, соединяющих вершину с другими вершинами. Важные вершины с высокой степенью обычно обладают большим влиянием в графе. Центральность по близости измеряет, как быстро вершина может достичь других вершин в графе. Чем меньше суммарное расстояние до всех других вершин, тем выше её близость.

Центральность посредничества оценивает, насколько часто вершина лежит на кратчайших путях между другими вершинами. Эта мера полезна для понимания узлов, которые служат «мостами» в сети, и их удаление может существенно повлиять на структуру графа. Собственная центральность, также известная как центральность на основе собственных векторов, определяет важность вершины с учётом её связи с другими важными вершинами в графе.

Для анализа графов в Python можно использовать библиотеку NetworkX, которая предоставляет удобные функции для выполнения всех этих операций. С помощью неё можно легко вычислить центральность, найти кратчайшие пути и исследовать другие аспекты структуры графа.

Вопрос-ответ:

Как создать граф с использованием Python?

Для создания графа в Python можно использовать библиотеку NetworkX. Она предоставляет простые инструменты для создания, манипулирования и анализа графов. Для начала достаточно импортировать NetworkX и создать пустой граф с помощью команды nx.Graph(). После этого можно добавлять вершины с помощью метода add_node() и ребра с помощью add_edge(). Граф можно визуализировать с помощью библиотеки Matplotlib.

Какие типы графов поддерживает библиотека NetworkX?

Библиотека NetworkX поддерживает несколько типов графов: направленные графы (DiGraph), неориентированные графы (Graph), многогранные графы (MultiGraph), где могут быть несколько ребер между двумя вершинами, и другие варианты. В зависимости от задач можно выбрать наиболее подходящий тип графа для работы.

Можно ли добавлять веса к ребрам графа в Python?

Да, библиотека NetworkX позволяет добавлять веса к ребрам графа. Веса можно указать при добавлении ребра, передав аргумент weight в метод add_edge(). Например: graph.add_edge(node1, node2, weight=4). Позже эти веса можно использовать при анализе графа, например, для нахождения кратчайшего пути между вершинами.

Как визуализировать граф в Python?

Для визуализации графа в Python часто используют библиотеку Matplotlib. После того как граф создан с помощью NetworkX, можно воспользоваться функцией nx.draw(), которая строит граф в окне Matplotlib. Для более сложных настроек визуализации, например, изменения цветов вершин или ребер, можно использовать дополнительные параметры, такие как node_color, edge_color, with_labels и другие.

Как можно найти кратчайший путь между двумя вершинами в графе с использованием Python?

Для нахождения кратчайшего пути в графе можно использовать встроенную функцию NetworkX nx.shortest_path(). Она использует алгоритм поиска пути по весам ребер. Например, для поиска кратчайшего пути между вершинами node1 и node2 можно использовать команду nx.shortest_path(graph, source=node1, target=node2). Если граф взвешенный, то нужно также указать параметр weight, чтобы учитывать веса ребер при расчете.