Таблицы истинности являются важным инструментом при изучении логики и теории вычислений. Они помогают наглядно представить работу логических выражений и выражают зависимость результата от значений переменных. Правильное составление таблицы истинности – это основа для глубокого понимания логических операций, таких как конъюнкция, дизъюнкция, импликация и другие.
Процесс составления таблицы истинности включает в себя несколько важных шагов. Для начала нужно определить количество переменных, которые участвуют в логическом выражении. От этого зависит количество строк в таблице. Каждая строка отражает одну возможную комбинацию значений переменных: истинно (1) или ложно (0). Следующий шаг – вычисление значения логических операций для каждой строки.
Чтобы правильно решить задачу с таблицей истинности, важно тщательно соблюдать порядок операций и учитывать приоритет логических связок. Для этого необходимо использовать известные правила и алгоритмы. Важно помнить, что точность выполнения каждого шага напрямую влияет на конечный результат.
Что такое таблица истинности и как ее использовать
Каждое выражение логики состоит из операндов и операторов. Операнды могут принимать значения истина или ложь, а операторы (например, AND, OR, NOT) определяют, как эти значения взаимодействуют между собой.
Использование таблицы истинности позволяет наглядно увидеть, как различные логические операторы влияют на итоговый результат. Для этого строится таблица, в которой указаны все возможные значения входных переменных и соответствующие им значения выражения.
Таблицы истинности широко применяются в информатике при анализе алгоритмов, создании логических схем и решении задач на логические выражения. Они особенно полезны при проектировании цифровых устройств, таких как схемы для вычислительных машин, где необходимо точно определить, как операторы будут работать в разных ситуациях.
Чтобы построить таблицу истинности, необходимо начать с указания всех возможных значений для переменных. Затем с помощью логических операторов вычисляются результаты для каждой строки таблицы. Полученные данные помогают понять, как выражение будет вести себя при различных комбинациях входных значений.
Таким образом, таблица истинности – это незаменимый инструмент для анализа логических выражений и их использования в различных областях информатики.
Алгоритм построения таблицы истинности для логических выражений
Для построения таблицы истинности логического выражения необходимо следовать определённому алгоритму. Первый шаг – выявить все переменные, входящие в выражение. Каждая из переменных может принимать одно из двух значений: истинно (1) или ложно (0).
Затем необходимо определить количество строк в таблице. Количество строк зависит от числа переменных и вычисляется по формуле 2^n, где n – количество переменных. Это связано с тем, что каждая переменная имеет два возможных значения, и для n переменных будет 2^n возможных комбинаций значений.
После этого строится список всех возможных комбинаций значений переменных. Обычно таблица начинается с комбинаций, где значение первой переменной меняется быстрее, а значение последней переменной – медленнее. Например, для двух переменных будет четыре комбинации: (0, 0), (0, 1), (1, 0), (1, 1).
Далее нужно пошагово вычислить значения логического выражения для каждой комбинации. Важно соблюдать приоритет операций: сначала выполняются операции с наибольшим приоритетом (например, отрицание), затем – операции с меньшим приоритетом (конъюнкция, дизъюнкция и т.д.).
После выполнения всех вычислений для каждой комбинации значений переменных заполняется соответствующий столбец в таблице истинности. В результате получается таблица, которая показывает все возможные результаты логического выражения для всех возможных значений переменных.
Как правильно учитывать приоритет операций в логических выражениях
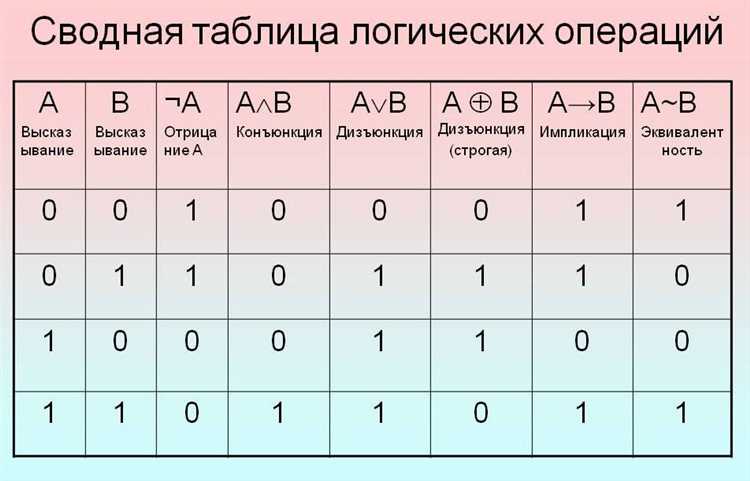
При решении логических выражений важно учитывать правильный приоритет операций, чтобы результат был верным. В логике существует несколько типов операций, и их приоритет определяет, в каком порядке они будут выполняться.
Основные логические операции включают AND (конъюнкция), OR (дизъюнкция), NOT (отрицание), а также скобки, которые могут изменять порядок выполнения операций. Без правильного порядка можно получить неверный результат.
В логических выражениях операция отрицания (NOT) имеет наивысший приоритет. Это значит, что она выполняется первой, независимо от того, что стоит после нее. Например, выражение NOT A AND B сначала будет выполнять отрицание A, а затем результат будет комбинироваться с B через операцию AND.
Операции AND и OR имеют более низкий приоритет по сравнению с NOT, но между ними AND выполняется раньше. Это означает, что в выражении A AND B OR C сначала будет выполнена операция AND между A и B, а затем результат будет подвергнут операции OR с C.
При наличии скобок приоритет операций изменяется. Сначала выполняются операции, заключенные в скобки, вне зависимости от их типа. Например, в выражении (A OR B) AND C сначала выполняется операция OR, и только потом результат будет использоваться в операции AND.
Важно помнить, что если в выражении несколько операций с одинаковым приоритетом, то они выполняются слева направо. Это правило касается операций AND и OR.
Таким образом, для правильного выполнения логического выражения необходимо соблюдать приоритет операций и использовать скобки, если порядок выполнения операций имеет значение для результата.
Как определять значения логических операций в таблице истинности
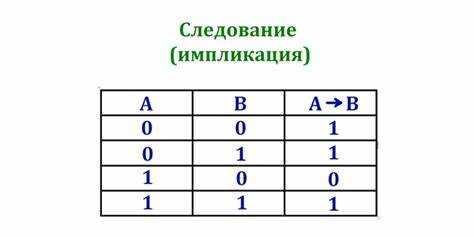
Для правильного определения значений логических операций в таблице истинности необходимо понимать основные логические операции: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание), импликация и эквиваленция. Каждая из них имеет свои особенности, которые важно учитывать при построении таблицы.
- Операция И (конъюнкция) возвращает истину, если оба операнда истинны. В остальных случаях результат будет ложным.
- Операция ИЛИ (дизъюнкция) возвращает истину, если хотя бы один из операндов истинный. Ложь будет, только если оба операнда ложны.
- Операция НЕ (отрицание) инвертирует значение операнда. Если входной параметр истинный, то результат будет ложным, и наоборот.
- Операция импликации (если A, то B) истинна во всех случаях, кроме того, когда A истинно, а B ложно.
- Операция эквиваленции (A эквивалентно B) возвращает истину, если оба операнда имеют одинаковые значения (оба истинны или оба ложны).
Для построения таблицы истинности необходимо перебрать все возможные комбинации значений исходных переменных и для каждой из них вычислить результат каждой логической операции. Результат заносится в таблицу по очереди.
Ошибки при решении таблиц истинности и как их избежать
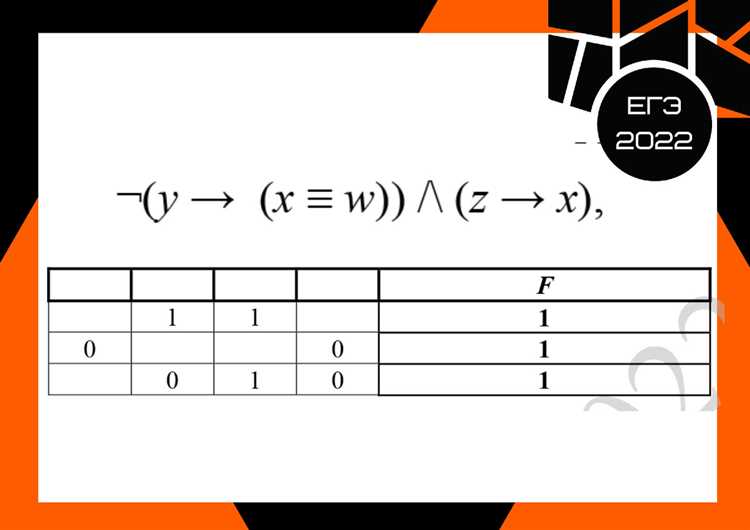
Решение таблиц истинности может быть сложным процессом, особенно для новичков. Вот несколько типичных ошибок и способы их избежать:
- Невнимательность при записи значений переменных – одна из распространенных ошибок. Часто можно забыть переписать все возможные комбинации значений для переменных, особенно когда их много. Чтобы избежать этой ошибки, всегда проверяйте, что все строки таблицы корректно заполнены.
- Ошибки в вычислениях логических операций – неправильный результат может появиться из-за невнимательности при вычислении операций И, ИЛИ, НЕ. Например, не стоит путать правила для И (операция возвращает истину только при обоих истинах). Чтобы избежать таких ошибок, рекомендуется помнить основные правила логики и внимательно следить за их применением.
- Неверное использование приоритетов операций – иногда при решении таблицы истинности можно ошибиться в очередности выполнения операций. Операция НЕ выполняется раньше, чем И и ИЛИ. Важно всегда соблюдать правильный порядок операций, чтобы избежать логических ошибок.
- Пропуск скобок – без скобок бывает сложно понять, какая операция должна быть выполнена первой. Всегда расставляйте скобки, если выражение сложное, чтобы не путаться в приоритетах.
- Недооценка количества строк таблицы – в случае с большим количеством переменных можно недооценить необходимое количество строк для всех возможных комбинаций. Для двух переменных нужно 4 строки, для трех – 8, и так далее. Проверьте, что количество строк совпадает с 2 в степени количества переменных.
- Отсутствие проверки – иногда, после вычисления всех значений, можно пропустить итоговую проверку таблицы на ошибки. Чтобы избежать этого, всегда пересматривайте готовую таблицу и внимательно проверяйте результаты.
Следуя этим рекомендациям, можно значительно снизить вероятность ошибок при решении таблиц истинности и сделать процесс более точным и быстрым.
Применение таблиц истинности для анализа логических выражений
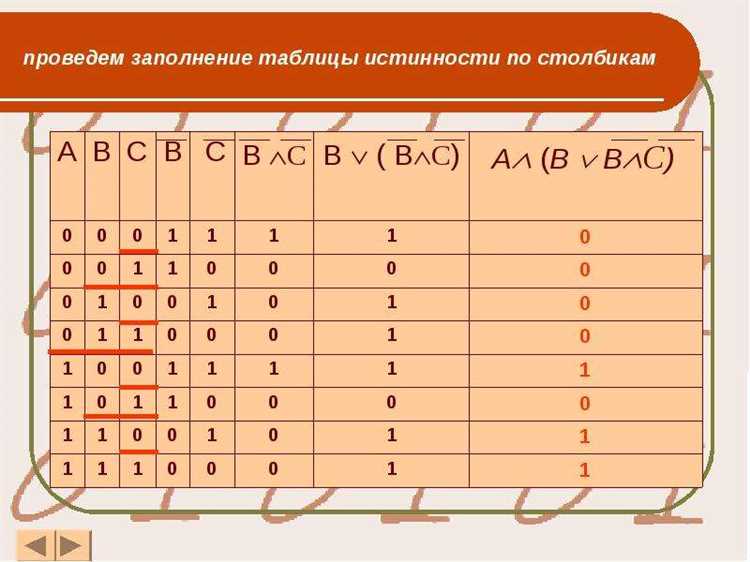
Таблицы истинности служат важным инструментом для анализа логических выражений, позволяя наглядно определить их поведение при разных значениях переменных. С помощью таблицы можно узнать, какие значения будут принимать логические операции при разных комбинациях значений входных переменных.
Для анализа логических выражений важно построить таблицу, в которой будут указаны все возможные комбинации истинности для исходных переменных. Затем для каждой комбинации вычисляются значения сложных логических операций, таких как «И», «ИЛИ», «НЕ», а также их сочетания. Это позволяет точно выявить, при каких условиях выражение будет истинным или ложным.
Таблицы истинности полезны для проверки эквивалентности выражений, поиска упрощений и выявления ошибок в логических формулах. Они также применяются для построения схем логических элементов, а также в области алгоритмов и программирования, где необходимо четко определить результат работы различных логических операций.
При решении более сложных выражений таблицы истинности помогают систематизировать процесс анализа, обеспечивая полное покрытие всех возможных ситуаций, что минимизирует вероятность ошибок и позволяет добиться точных результатов.
Решение сложных логических выражений: использование дополнительных методов
Другим полезным инструментом является метод приведения выражений к каноническим формам, таким как нормальная форма ДНФ (дизъюнктивная нормальная форма) и КНФ (конъюнктивная нормальная форма). В этих формах выражения легче анализировать, а также они являются удобными для дальнейших вычислений или оптимизации логических схем.
Для упрощения логических выражений также можно использовать таблицы истинности для отдельных частей выражения, а не для всего выражения целиком. Это позволяет локализовать сложности и быстрее находить решение.
Кроме того, полезным методом является метод булевой алгебры, который позволяет с помощью алгебраических преобразований свести сложные выражения к более простым. Например, используя такие операции, как исключающее ИЛИ (XOR) или операции инверсии, можно сократить количество операций и упростить логическую схему.
Вопрос-ответ:
Что такое таблица истинности и для чего она используется в информатике?
Таблица истинности — это таблица, которая показывает все возможные значения логических выражений, используемых в логике высказываний или булевой алгебре. В таких таблицах обычно указываются все возможные комбинации значений входных переменных и соответствующие значения результата для логических операций (например, И, ИЛИ, НЕ). Таблицы истинности необходимы для анализа логических выражений, упрощения формул и понимания работы логических схем в различных приложениях, от цифровых вычислений до проектирования компьютерных программ.
Как построить таблицу истинности для сложного логического выражения?
Чтобы построить таблицу истинности для сложного логического выражения, нужно выполнить несколько шагов. Сначала определите все переменные, участвующие в выражении. Затем составьте таблицу, где укажите все возможные комбинации значений этих переменных (например, для двух переменных будет 4 строки: 00, 01, 10, 11). После этого последовательно вычисляйте значения логических операций, начиная с самых простых (например, НЕ, ИЛИ, И), и заканчивайте результатом всего выражения. Таким образом, каждая строка в таблице будет представлять собой один случай для конкретного выражения.
Что делать, если выражение содержит несколько логических операций, и как правильно их расставлять?
Когда выражение включает несколько логических операций, важно помнить приоритет операторов. Операции, такие как отрицание (НЕ), имеют более высокий приоритет и выполняются первыми. Далее идут операции «И» (AND), а затем «ИЛИ» (OR). Таким образом, перед тем как строить таблицу истинности, важно расставить скобки, если это необходимо, чтобы точно понять, какая операция выполняется первой. После этого можно шаг за шагом разбирать выражение, используя таблицу для каждой операции, начиная с самой вложенной.
Как правильно использовать таблицу истинности при упрощении логических выражений?
Таблица истинности помогает при упрощении логических выражений, поскольку она показывает, при каких значениях переменных выражение дает истинное или ложное значение. Используя таблицу, можно выявить эквивалентные логические выражения или оптимизировать их, заменяя сложные операции более простыми. Например, можно проверить, когда результат операции всегда истинный или ложный, что помогает выделить бессмысленные части выражения и упростить его. Это особенно полезно при проектировании цифровых схем или при оптимизации программного кода.
Есть ли какие-то особенности при составлении таблицы истинности для операций с несколькими переменными?
При составлении таблицы истинности для операций с несколькими переменными важно учесть количество строк в таблице, которое зависит от количества переменных. Для n переменных будет 2^n строк. Чем больше переменных, тем сложнее и объемнее становится таблица. Важно помнить, что для каждой строки таблицы необходимо вычислить результат всех логических операций для данной комбинации значений переменных. Поскольку таблицы с большим количеством переменных могут быть громоздкими, иногда используют упрощенные методы, такие как применение законов логики для сокращения количества операций.
Что такое таблица истинности и для чего она используется в информатике?
Таблица истинности — это математическое представление логических выражений, где для каждой возможной комбинации значений переменных указывается результат выражения. Она применяется для анализа и построения логических схем, а также в программировании для проверки корректности логических операций. Таблицы истинности используются в изучении логики, алгебры и в области теории вычислений, помогая понять, как различные логические операции ведут себя при разных значениях входных данных.
Как правильно заполнять таблицу истинности для логического выражения?
Для того чтобы правильно заполнить таблицу истинности, нужно следовать нескольким шагам. Сначала необходимо определить количество переменных в выражении. Например, для выражения с двумя переменными, таблица будет состоять из 4 строк (так как возможны 4 комбинации значений: истинно или ложно для каждой переменной). Далее, на основе логических операций (И, ИЛИ, НЕ и т.д.) поочередно вычисляются значения выражения для каждой комбинации входных данных. Пример: для выражения «A И B» истинность будет установлена только тогда, когда обе переменные будут истинными. Важным моментом является последовательность вычислений — операции с приоритетом должны выполняться первыми (например, сначала NOT, потом AND, затем OR).