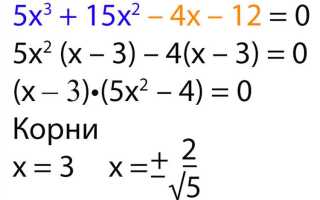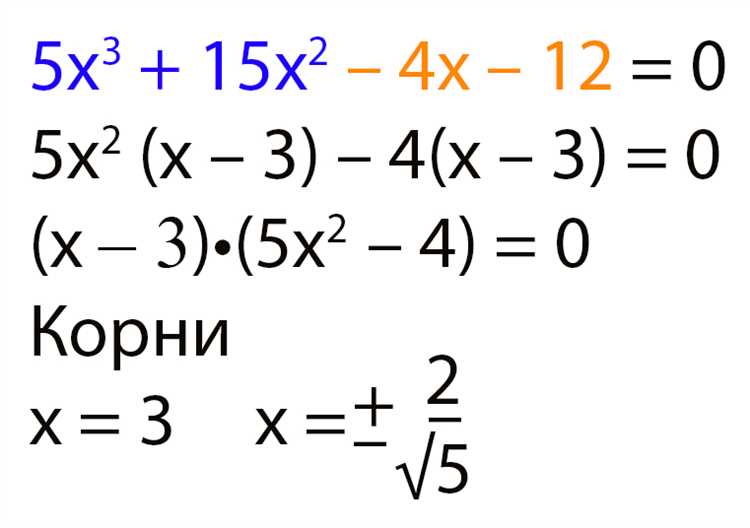
Программное обеспечение Matcad является мощным инструментом для решения математических задач, анализа данных и визуализации. Одной из основных возможностей этой программы является решение уравнений. В данном руководстве будет рассмотрен процесс решения уравнений с использованием Matcad, включая пошаговые инструкции для различных типов уравнений.
Matcad позволяет не только находить аналитические решения, но и численные значения, что значительно облегчает работу с сложными математическими выражениями. Программа поддерживает различные методы решения, от простых алгебраических уравнений до более сложных дифференциальных уравнений. Для того чтобы использовать этот инструмент, необходимо понимать основные принципы работы в Matcad и последовательность действий при решении уравнений.
В следующих разделах вы узнаете, как настроить рабочее пространство для решения уравнений, какие функции использовать для разных типов задач, а также как интерпретировать результаты. Это руководство будет полезно как для новичков, так и для более опытных пользователей программы.
Решение уравнений в Маткаде: пошаговая инструкция

- Запуск программы
Откройте программу Маткад на вашем компьютере.
- Ввод уравнения
Для начала введите уравнение в рабочем пространстве Маткада. Например, для уравнения x^2 — 5 = 0 введите его в строку команд.
- Использование функции solve
Для решения уравнений используйте встроенную функцию solve. Введите команду вида:
solve(x^2 — 5 = 0, x)
- Запуск решения
Нажмите клавишу Enter, чтобы Маткад выполнил решение. Результаты появятся в рабочем пространстве.
- Проверка решения
Проверьте правильность полученных решений, подставив их обратно в исходное уравнение.
- Визуализация решений
Для визуализации решения уравнения можно использовать графики. Для этого введите команду для построения графика функции.
- Дополнительные настройки
Если необходимо, измените параметры решения, такие как точность или диапазон значений переменных.
В результате вы получите решение уравнения с возможностью дальнейшего анализа и проверки.
Как настроить рабочее пространство для решения уравнений в Маткаде

Для эффективной работы с уравнениями в Маткаде необходимо правильно настроить рабочее пространство. Это позволит ускорить процесс и минимизировать ошибки. Следуйте инструкциям, чтобы подготовить Маткад к решению уравнений.
- Откройте программу и создайте новый рабочий файл, выбрав «Новый документ» в главном меню.
- На панели инструментов выберите режим «Рабочая страница» для удобства ввода уравнений.
- Настройте параметры документа. Для этого перейдите в раздел «Файл» и выберите «Настройки». Убедитесь, что установлены нужные единицы измерения и точность расчетов.
- Для решения уравнений используйте поле «Командная строка». Здесь можно вводить математические выражения и устанавливать переменные.
После этого вы можете приступить к решению уравнений, вводя их в соответствующие ячейки или используя команды для численного или символьного решения.
- Добавьте необходимые библиотеки или модули, если это требуется для решения более сложных уравнений.
- Для работы с графиками уравнений, активируйте окно «График», чтобы визуализировать результаты.
Настройка рабочего пространства в Маткаде позволяет оптимизировать процесс решения уравнений и повысить точность расчетов.
Ввод уравнений в Маткаде с использованием символов и операторов
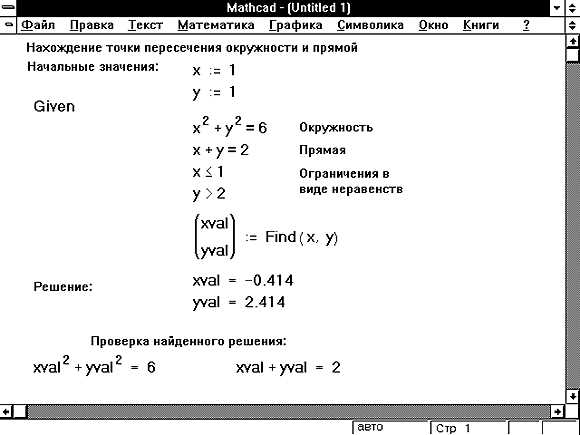
Для ввода уравнений в Маткаде необходимо использовать соответствующие символы и операторы. Уравнение может быть записано с использованием переменных, чисел и математических операций. Переменные в Маткаде задаются с помощью букв, например, x, y, z, и могут быть определены как числовые значения или функции.
Для выполнения математических операций используются стандартные операторы, такие как:
- + – сложение
- — – вычитание
- * – умножение
- / – деление
- ^ – возведение в степень
- = – знак равенства, используемый для задания уравнений
Пример простого уравнения: x + y = 10.
Также в Маткаде доступны более сложные операторы и функции, такие как интегралы, производные, логарифмы и тригонометрические функции. Например, для записи производной функции f(x) по переменной x используется оператор diff, что выглядит как diff(f(x), x).
Для задания уравнений с несколькими переменными или параметрами можно использовать систему уравнений. Это можно сделать, просто записав несколько уравнений в одной строке, разделяя их точкой с запятой. Например: x + y = 10; x — y = 2.
Маткад автоматически решает такие системы уравнений, если переменные заданы корректно, и предоставляет решение в виде значений для переменных.
Пошаговый процесс нахождения корней уравнений в Маткаде

Шаг 1: Определение уравнения
Первоначально нужно ввести уравнение, корень которого требуется найти. Для этого откройте новый документ в Маткаде и введите уравнение в соответствующем формате. Например, для уравнения вида f(x) = 0, где f(x) – функция, необходимо ввести выражение для f(x).
Шаг 2: Инициализация переменных
Задайте переменную, для которой нужно найти значение. Обычно это переменная x, но в зависимости от задачи могут использоваться и другие символы. Пример: x := 0.
Шаг 3: Применение функции решения
Для нахождения корня используйте функцию solve. Введите команду для поиска корня уравнения: solve(f(x) = 0, x). Эта команда инициирует процесс поиска решения для переменной x.
Шаг 4: Анализ результатов
После выполнения команды Маткад отобразит найденные корни уравнения. Если корень существует, система выведет его значение. Важно проверить, не является ли решение комплексным или неподходящим для задачи.
Шаг 5: Дополнительные проверки
Если у уравнения несколько корней, Маткад может предложить несколько решений. В этом случае можно использовать дополнительные условия, например, ограничить диапазон значений для x или уточнить тип решения.
Шаг 6: Проверка точности решения
Для проверки точности решения уравнения можно использовать функцию evalf, которая позволяет получить численное значение корня с заданной точностью.
Решение систем линейных уравнений с помощью Маткада
Для решения системы линейных уравнений в Маткаде используется команда linsolve. С помощью этой функции можно найти решение системы, состоящей из нескольких линейных уравнений с несколькими переменными.
Рассмотрим пример системы линейных уравнений:
3x + 2y = 5
4x — y = 6
Чтобы решить эту систему в Маткаде, выполните следующие шаги:
1. Введите коэффициенты системы как матрицу. Коэффициенты для системы уравнений можно представить в виде матрицы A:
A := [3 2; 4 -1]
2. Задайте столбец с правыми частями уравнений. Это будет вектор B:
B := [5; 6]
3. Для получения решения системы используйте команду linsolve, которая принимает матрицу коэффициентов и вектор правых частей:
Решение будет найдено следующим образом:
x := linsolve(A, B)
4. Вектор x будет содержать значения переменных x и y, которые удовлетворяют системе уравнений.
x = [2; 1]
Это означает, что x = 2 и y = 1 – решение данной системы уравнений.
Использование численных методов для решения уравнений в Маткаде
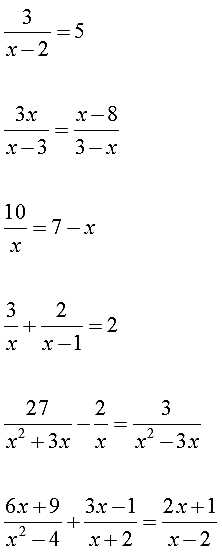
Другим популярным методом является метод деления пополам, который основан на принципе последовательного сужения интервала, в котором содержится корень. Он подходит для решений уравнений, когда функция имеет конечное количество корней и можно определить начальный интервал.
В Маткаде также доступен метод секущих, который является улучшением метода Ньютона. Он требует меньше вычислений, так как не требует вычисления производных функции, но может иметь меньшую скорость сходимости.
Для решения систем нелинейных уравнений Маткад предлагает использование метода Гаусса-Зейделя и метода подбора, что особенно полезно для задач с несколькими переменными. Эти методы позволяют найти решение системы уравнений, используя итерационные подходы, которые постепенно приближаются к точному результату.
Для каждой из этих задач в Маткаде можно настроить параметры точности и количество итераций, что позволяет контролировать процесс решения и избегать излишней вычислительной нагрузки. Численные методы в Маткаде обеспечивают гибкость и точность, что делает их удобным инструментом для решения различных типов уравнений.
Как задать начальные условия и ограничения для решения уравнений
Для корректного решения уравнений в Matcad необходимо задать начальные условия и ограничения, которые помогут системе правильно интерпретировать задачу. Начальные условия определяют значения переменных на начальном шаге решения, а ограничения помогают системе учитывать допустимые диапазоны значений для переменных.
Чтобы задать начальные условия в Matcad, нужно просто присвоить значения переменным. Например, для задания начальных значений переменных x и y можно использовать следующий код:
x := 0 y := 5
Кроме того, важно определить ограничения для переменных, чтобы исключить недопустимые значения. Для этого можно использовать условные операторы. Например, чтобы ограничить переменную x значением от 0 до 10, можно использовать следующий код:
x >= 0 and x <= 10
Ограничения могут быть применены и к функциям. В таких случаях можно задать диапазоны, в которых функция должна быть определена. Например, если решение уравнения зависит от функции f(x), которая определена только для положительных значений x, это можно задать так:
f(x) := sqrt(x) for x >= 0
Важно также учитывать ограничения на параметры, которые могут изменяться в процессе решения. Например, для числовых методов решения можно указать максимальное количество итераций, точность или пределы изменения переменной, чтобы гарантировать, что решение будет получено в пределах заданных условий.
Корректно заданные начальные условия и ограничения позволяют избежать ошибок при решении уравнений и обеспечивают более точный и быстрый процесс вычислений.
Интерпретация и визуализация результатов решений в Маткаде

Для интерпретации результатов в Маткаде важно ознакомиться с числами или выражениями, полученными в процессе вычислений. В случае численных решений, результат может быть представлен в виде простого числа, которое легко воспринимается. Однако для более сложных уравнений, например, в случае аналитических решений, результат может быть в виде выражений, которые требуют дополнительной проверки и анализа.
Визуализация результатов позволяет представить данные в графической форме. Это могут быть графики, диаграммы или 3D-построения. Маткад предоставляет инструменты для создания графиков, где можно отобразить зависимость одной переменной от другой, а также выполнить настройку осей, цветов и типов графиков. Визуализация помогает наглядно оценить поведение решений в разных условиях.
Графики и диаграммы являются мощным инструментом для анализа данных, так как позволяют быстро выявить закономерности и аномалии. Например, для уравнений, содержащих переменные, которые зависят от времени, можно построить график, отображающий изменение значений переменных в процессе времени. Это позволяет увидеть динамику изменений и принять более обоснованные решения.
Кроме того, Маткад предоставляет возможность отображать решения в виде таблиц или числовых значений, которые могут быть полезны для дальнейших вычислений или отчетности. Все результаты могут быть легко экспортированы в различные форматы для дальнейшей работы в других приложениях.
Визуализация помогает не только интерпретировать результаты, но и улучшить представление о их значении, что делает процесс анализа более эффективным и понятным.
Вопрос-ответ:
Как начать решать уравнения в Маткаде?
Чтобы начать решать уравнения в Маткаде, необходимо сначала установить программу на свой компьютер. После этого откройте новый рабочий лист и выберите инструмент для работы с уравнениями. В Маткаде можно вводить математические выражения и решать их с помощью встроенных функций. Введите уравнение в соответствующем формате и воспользуйтесь командой решения для нахождения корней.
Как решить систему уравнений в Маткаде?
Для решения системы уравнений в Маткаде нужно использовать функции для работы с матрицами. Сначала задайте систему в виде матрицы коэффициентов и вектора свободных членов. Затем используйте команду `linsolve` для нахождения решения этой системы. Результатом будет вектор, содержащий значения переменных системы.
Как использовать функцию для нахождения корней уравнений в Маткаде?
В Маткаде есть несколько методов для нахождения корней уравнений. Одним из них является использование функции `fsolve`. Для этого нужно ввести уравнение и задать начальное приближение. Функция будет искать корень уравнения в заданной области. Результат можно увидеть на экране, и он будет точным в зависимости от точности вычислений.
Что делать, если уравнение не решается в Маткаде?
Если уравнение не решается, сначала проверьте правильность его ввода: используйте правильные математические операторы и соблюдайте синтаксис. Также возможно, что уравнение не имеет решения или имеет несколько решений. В таких случаях можно попробовать задать различные начальные условия или воспользоваться другими методами решения, например, численными методами, если аналитическое решение невозможно.
Какие типы уравнений можно решать в Маткаде?
В Маткаде можно решать различные типы уравнений, включая линейные, нелинейные, алгебраические, дифференциальные и интегральные уравнения. Для каждого типа уравнений существуют свои функции и методы решения. Программа позволяет работать как с простыми уравнениями, так и с более сложными задачами, требующими численных методов.
Как решить уравнение в Маткаде?
Чтобы решить уравнение в Маткаде, необходимо выполнить несколько шагов. Во-первых, нужно ввести само уравнение в рабочее поле программы. Для этого используйте соответствующие символы для переменных и операторов. Далее, укажите, что нужно решить, используя функцию `solve` или другую подходящую команду, если это необходимо. Также важно задать значения переменных, если это необходимо для правильного решения. После этого Маткад выполнит вычисления и выведет решение. Чтобы увидеть все этапы решения, можно использовать блоки вычислений, такие как `assume` или `simplify`, для упрощения выражений и получения наглядных результатов.