Как возвести в степень в pascal

В языке программирования Pascal возведение числа в степень можно реализовать с использованием встроенных операторов и функций. В большинстве случаев для решения этой задачи используется оператор умножения в цикле или стандартная функция для работы с математическими операциями.

Одним из самых прямых методов является создание цикла, который будет многократно умножать число на себя. Это можно легко реализовать с помощью конструкций for или while. Такой способ требует от программиста явного контроля за количеством операций умножения.

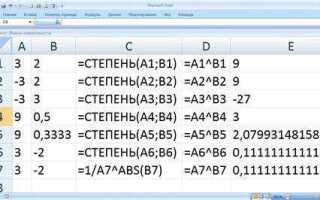
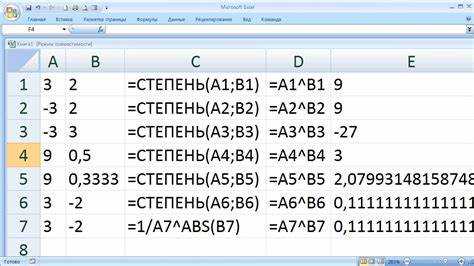
Однако существует более удобный способ – использование функции power, которая предоставляет стандартная библиотека Pascal. Эта функция принимает два аргумента: основание и показатель степени, и автоматически вычисляет результат. Например, power(2, 3) вернет 8.

В случае использования функции power важно учитывать, что она работает с вещественными числами, поэтому результат всегда будет типа real, даже если оба аргумента целые.

Для улучшения производительности при больших степенях можно использовать алгоритмы быстрого возведения в степень, такие как метод «деления и властвования», который значительно сокращает количество операций умножения.

Использование оператора возведения в степень в Pascal

В Pascal для возведения числа в степень используется функция Power, которая входит в стандартную библиотеку языка. Эта функция позволяет вычислять степень числа с использованием двух аргументов: основания и показателя степени. Рассмотрим основные моменты работы с этой функцией.

Синтаксис функции выглядит следующим образом:

Power(основание, показатель)

Где:

• основание – число, которое возводится в степень;
• показатель – степень, в которую возводится основание (целое или действительное число).

Пример использования функции Power:

var
result: Real;
begin
result := Power(2, 3);
end.

Если требуется возвести число в степень с целым показателем, результат будет целым числом. В случае с действительным числом результат будет типа Real.

Также возможен вариант возведения числа в степень с использованием целочисленных значений, однако функция Power возвращает результат типа Real, что следует учитывать при вычислениях с целыми числами.

Некоторые особенности:

• Если основание отрицательное, а показатель степени является дробным числом, то функция может вернуть ошибку, так как результат может быть комплексным;
• При возведении числа в степень 0 результат всегда равен 1 (за исключением случая с основанием 0, где результат неопределен);
• Функция Power из библиотеки Math не поддерживает комплексные числа, для работы с ними требуется использование дополнительных библиотек.

Возведение числа в степень в Pascal позволяет легко выполнять операции с числами любой сложности, при этом важно правильно обрабатывать возможные исключения и ошибки при вычислениях.

Как вычислить степень с использованием функции Power

В Pascal для возведения числа в степень можно использовать встроенную функцию Power. Эта функция доступна в модуле Math и имеет следующий синтаксис:

Power(основание, показатель);

Где основание – это число, которое будет возводиться в степень, а показатель – степень, в которую это число нужно возвести. Функция возвращает значение типа Real.

Пример использования:

uses Math;
var
result: Real;
begin
result := Power(2, 3);
end.

В этом примере число 2 возводится в степень 3, что дает результат 8. Функция Power позволяет работать не только с целыми числами, но и с вещественными значениями, что делает её гибким инструментом для математических операций.

Особенности:

• Функция может работать с отрицательными показателями степени, например, Power(2, -1) вернёт 0.5.
• Если основание – 0, а показатель отрицательный, программа вызовет ошибку деления на ноль.
• Результат всегда имеет тип Real, даже если основание и показатель целые.

Для простых вычислений степени лучше использовать именно эту функцию, так как она оптимизирована для работы с числами и поддерживает более широкий диапазон значений по сравнению с ручными вычислениями с помощью цикла или рекурсии.

Обработка отрицательных и нулевых экспонент в Pascal

В языке Pascal возведение числа в степень с отрицательной или нулевой экспонентой требует особого подхода для корректного выполнения операции. Рассмотрим, как это можно реализовать и какие моменты нужно учитывать.

При возведении числа в нулевую степень результат всегда равен 1, независимо от значения основания, если основание не равно нулю. Для отрицательных экспонент необходимо учитывать, что результат будет равен обратному числу, возведенному в положительную степень.

• Для нулевой экспоненты результат всегда равен 1, если основание не равно нулю.
• Если основание равно нулю, то возведение в нулевую степень приводит к неопределенности (делению на ноль), что может вызвать ошибку выполнения.
• Отрицательная экспонента означает нахождение обратного числа. Например, x^(-n) эквивалентно 1 / (x^n), где n – положительное целое число.
• Если основание равно нулю, отрицательная экспонента приводит к ошибке деления на ноль.

В Pascal возведение числа в отрицательную степень можно реализовать через явное использование операции деления. Например, для вычисления x^(-n) можно воспользоваться следующим подходом:

function Power(x: Real; n: Integer): Real;
begin
if n = 0 then
Power := 1
else if n > 0 then
Power := x * Power(x, n - 1)
else
Power := 1 / Power(x, -n);
end;

В этой функции обработка отрицательной экспоненты осуществляется путем рекурсивного вызова функции с положительным значением экспоненты и делением на результат. Для нулевой экспоненты просто возвращается 1.

Необходимо учитывать, что при использовании вещественных чисел для возведения в отрицательную степень значение 0 в качестве основания вызовет ошибку выполнения. Рекомендуется добавлять дополнительные проверки на ноль перед выполнением операции для предотвращения деления на ноль.

Реализация возведения числа в степень через цикл

Для возведения числа в степень можно использовать цикл. Этот метод особенно полезен, когда необходимо избежать использования встроенных операторов или функций. В языке Pascal цикл позволяет последовательно умножать число на себя несколько раз, что эквивалентно возведению его в степень.

Основная идея заключается в том, чтобы зафиксировать основание числа и многократно умножать его на себя, пока не будет достигнут нужный показатель степени. Алгоритм работает следующим образом: начиная с единицы, мы поочередно умножаем результат на основание, пока не пройдет заданное количество итераций.

Пример кода для возведения числа в степень с помощью цикла for:

program PowerCalculation;
var
base, exponent, result, i: integer;
begin
Write('Введите основание: ');
ReadLn(base);
Write('Введите степень: ');
ReadLn(exponent);
result := 1;
for i := 1 to exponent do
result := result * base;
WriteLn('Результат: ', result);
end.

В данном примере base – это основание, а exponent – степень. В цикле переменная result начинает с единицы и в каждой итерации умножается на основание. Как только цикл завершает работу, переменная result содержит результат возведения числа в степень.

Важно учитывать, что данный подход работает только с целыми числами. Для работы с дробными значениями можно использовать тип данных real, но в этом случае потребуется учитывать возможные ошибки при округлении.

Использование цикла для возведения числа в степень имеет преимущество в простоте и прозрачности кода, однако для больших степеней эффективность такого метода может быть снижена. В таких случаях полезно рассмотреть более оптимизированные методы, такие как бинарное возведение в степень.

Вычисление степени с использованием рекурсии

Основная идея рекурсии при возведении числа в степень заключается в том, чтобы разбить задачу на более мелкие шаги. Например, для вычисления A^n можно представить выражение как A * A^(n-1), где степень уменьшается на 1 на каждом шаге, пока не достигнем степени 0, которая равна 1.

Пример функции на Pascal, использующей рекурсию для вычисления степени:

function Power(A: Integer; N: Integer): Integer;
begin
if N = 0 then
Power := 1
else
Power := A * Power(A, N - 1);
end;

Здесь функция Power принимает два параметра: основание A и степень N. Когда степень равна 0, функция возвращает 1 (по определению степени). В противном случае происходит рекурсивный вызов функции с уменьшенной на единицу степенью.

Важно учитывать, что рекурсивные функции могут быть менее эффективными, чем итеративные, особенно для больших значений степени. Каждый рекурсивный вызов требует дополнительной памяти для хранения контекста функции, что может привести к переполнению стека, если степень слишком велика.

Для оптимизации можно использовать технику, называемую быстрое возведение в степень. Эта техника сводит количество рекурсивных вызовов к минимуму, путем разделения степени на более мелкие компоненты. Например, для четных значений степени можно использовать следующий алгоритм:

function FastPower(A: Integer; N: Integer): Integer;
begin
if N = 0 then
FastPower := 1
else if N mod 2 = 0 then
FastPower := FastPower(A * A, N div 2)
else
FastPower := A * FastPower(A, N - 1);
end;

Этот метод уменьшает количество операций за счет использования свойств степени для ускорения вычислений. Это позволяет значительно повысить производительность при больших значениях N.

Ошибки при возведении в степень и как их избежать

При работе с возведением чисел в степень в Pascal часто встречаются ошибки, которые могут привести к неправильным результатам или сбоям в программе. Рассмотрим основные из них и способы их избегания.

1. Неверный тип данных

Возведение в степень требует использования подходящего типа данных. Например, если возводить число с плавающей запятой в степень, а тип переменной – целочисленный, результат может быть неточным или вовсе привести к ошибке компиляции. Чтобы избежать этого, всегда проверяйте типы данных перед выполнением операции. Для вещественных чисел используйте тип Real, для целых чисел – Integer.

2. Отрицательные показатели степени

Попытка возвести число в отрицательную степень без предварительной проверки может вызвать ошибку деления на ноль, если основание степени равно нулю. Чтобы избежать этого, необходимо предусмотреть проверку на ноль перед возведением в степень с отрицательным показателем.

3. Работа с нулевыми и единичными основаниями

Возведение нуля в нулевую степень или единицы в любую степень не вызывает ошибок, но может привести к логическим ошибкам в программе. Например, 0^0 считается неопределенным в математике. Для таких случаев желательно добавлять проверки на эти условия и обрабатывать их отдельно.

4. Переполнение при больших степенях

При вычислении больших степеней могут возникнуть проблемы с переполнением. Например, возведение числа 2 в степень 1000 выходит за пределы типа Integer. Для работы с большими степенями используйте типы данных с большей точностью, такие как Int64 или Real, или применяйте алгоритмы, которые могут работать с большими числами без переполнения.

5. Ошибки в вычислении степени с плавающей запятой

В случае работы с числами с плавающей запятой, округление и погрешности могут приводить к некорректным результатам. Чтобы уменьшить ошибки округления, используйте математические функции, такие как Exp и Ln, для более точных вычислений. Также полезно настроить точность вычислений через системные параметры или библиотеки для работы с числами высокой точности.

Возведение в степень для вещественных чисел

В Pascal возведение числа в степень выполняется с помощью встроенной функции Power. Эта функция позволяет работать с вещественными числами, возвращая результат в виде вещественного значения. Синтаксис выглядит так:

Power(число, степень)

Где число – это основание, а степень – показатель степени. Оба параметра должны быть вещественными числами (типа Real).

Пример возведения числа в степень:

Var
result: Real;
Begin
result := Power(2.5, 3);
WriteLn(result);  { Результат: 15.625 }
End.

Функция Power поддерживает любые вещественные значения как для основания, так и для показателя степени. Однако важно помнить, что при возведении в степень отрицательных чисел с нецелыми показателями может возникнуть ошибка из-за невозможности извлечения корня из отрицательного числа.

Для решения таких проблем можно заранее проверять знак числа и корректировать степень. Например, для отрицательных чисел можно использовать функцию Sqr для возведения в квадрат и т. д.

Также, если необходимо работать с вещественными числами, где основание меньше 1 и степень отрицательная, то результат будет выражаться как дробное число. Важно учитывать точность вычислений, так как вещественные числа в Pascal хранятся с ограниченной точностью, что может влиять на результаты при больших степенях.

Оптимизация вычислений при возведении в степень в Pascal

Алгоритм быстрого возведения в степень основан на разделении показателя степени на два, что позволяет значительно уменьшить количество операций. Вместо того чтобы вычислять число через последовательное умножение, степень делится на два, и результат собирается за логарифмическое количество шагов.

Пример реализации этого метода в Pascal:

function Power(base: Integer; exponent: Integer): Integer;
var
result: Integer;
begin
result := 1;
while exponent > 0 do
begin
if exponent mod 2 = 1 then
result := result * base;
base := base * base;
exponent := exponent div 2;
end;
Power := result;
end;

Этот алгоритм работает за время O(log n), где n – это показатель степени. Используя этот подход, можно существенно ускорить вычисления по сравнению с наивной реализацией, которая имеет время работы O(n).

Кроме того, при возведении в степень часто встречается необходимость работать с большими числами. В таких случаях полезно использовать типы данных с произвольной точностью, если они доступны в вашем компиляторе, или же интегрировать библиотеки для работы с длинными целыми числами.

Для оптимизации вычислений стоит также учитывать, что можно заранее вычислить значения для некоторых степеней чисел, если степень часто повторяется в программе. Это может быть полезно в задачах, где требуется многократное использование одинаковых значений степени.

При работе с числами с плавающей запятой стоит помнить о погрешностях, возникающих при использовании стандартных типов данных. Для точных вычислений лучше использовать специализированные типы или дополнительные библиотеки, обеспечивающие точность вычислений до требуемой степени.

Вопрос-ответ:

Как в Pascal возвести число в степень?

В Pascal для возведения числа в степень можно использовать операцию возведения в степень с помощью встроенной функции `Power`. Она принимает два аргумента: основание и показатель степени. Например, чтобы возвести число 2 в степень 3, код будет таким: `Power(2, 3)`. Это вернет результат 8.

Как работает функция Power в Pascal?

Функция `Power` в Pascal является частью стандартной библиотеки и используется для возведения числа в степень. Она работает следующим образом: принимает два аргумента — основание (число) и показатель степени (целое или вещественное число). Например, `Power(2, 3)` вернет 8. Стоит отметить, что результат будет вещественным числом, даже если оба аргумента — целые числа.